集合 Set

集合（Set）是由一组无序且唯一(即不能重复)的项（也可能是 0 个）组成的。该数据结构使用了与有限集合相同的数学概念，但应用在计算机科学的数据结构中。

在数学中，集合是一组不同对象的集，比如说，一个由大于或等于 0 的整数组成的自然数集：N = {0, 1, 2, 3, 4, 5, 6, ...}。集合中的对象列表用花括号（{}）包围。而不包含任何元素的集合叫做空集，空集用 { } 表示。

提示

可以把集合想象成一个既没有重复元素，也没有顺序概念的数组。

实现集合类

这里使用对象而不是数组来表示集合(items)，因为 JavaScript 的对象不允许一个键指向两个不同的属性，也保证了集合里的元素都是唯一的。当然也可以用数组实现。

需要声明一些集合可用的方法：

add(element)：向集合添加一个新元素。
delete(element)：从集合移除一个元素。
has(element)：如果元素在集合中，返回 true，否则返回 false。
clear()：移除集合中的所有元素。
size()：返回集合所包含元素的数量。它与数组的 length 属性类似。
values()：返回一个包含集合中所有值(元素)的数组。

class Set {
  constructor() {
    this.items = {};
  }

  /**
   * 添加元素
   */
  add(element) {
    // 调用 has 方法判断 element 是否存在于集合中
    if (!this.has(element)) {
      // 如果不存在，就把 element 添加到集合中
      // 添加 element 的时候，同时作为键和值保存，这样有利于查找该元素
      this.items[element] = element;
      // 返回 true 表示添加成功
      return true;
    }
    // 返回 false 表示未添加成功
    return false;
  }

  /**
   * 删除元素
   */
  delete(element) {
    // 是否存在
    if (this.has(element)) {
      // 存在，移除
      delete this.items[element];
      return true;
    }
    // 不存在
    return false;
  }

  /**
   * 检验某个元素是否存在于集合中
   */
  has(element) {
    // 方法一：用 JavaScript 的 in 运算符来验证给定元素是否是 items 对象的属性
    // return element in items;
    // 方法二：hasOwnProperty 方法返回一个表明对象是否具有特定属性的布尔值，而 in 会在原型链上查找
    return Object.prototype.hasOwnProperty.call(this.items, element);
  }

  /**
   * 获取所有元素值
   */
  values() {
    // 第一种：迭代 items 对象的自身所有属性（hasOwnProperty(key)，把它们添加到一个数组中并返回
    // 第二种：Object.values()方法返回了一个包含给定对象所有属性值的数组（ES2017 添加）
    // 使用 Object 类内置的 values 方法
    return Object.values(this.items);
  }

  /**
   * 获取集合中有元素个数
   */
  size() {
    // 第一种方式是使用一个 length 变量，每当使用 add 或 delete 方法时就控制它
    // 第二种第三种方式是迭代 items 对象的每一个属性，统计个数。（hasOwnProperty(key)判断当前对象属性）
    // 第三种方式是使用 Object 类的一个 ES6 中的 keys 方法
    // keys 方法，它返回一个包含给定对象所有属性的数组。集合元素个数这个数组的 length
    return Object.keys(this.items).length;
  }

  /**
   * 移除集合中的所有值
   */
  clear() {
    // 1. 可以迭代集合，用 delete 方法依次移除所有的值
    // 2. 重新赋值为空对象
    this.items = {};
  }
}

测试 Set 类

const set = new Set();

set.add(1);
console.log(set.values()); // 输出 [1]
console.log(set.has(1)); // 输出 true
console.log(set.size()); // 输出 1

set.add(2);
console.log(set.values()); // 输出 [1, 2]
console.log(set.has(2)); // 输出 true
console.log(set.size()); // 输出 2

set.delete(1);
console.log(set.values()); // 输出 [2]

set.delete(2);
console.log(set.values()); // 输出 []

集合运算

集合被用于关系数据库查询的设计和处理，如：获取某表中全部数据还是获取其中的子集；SQL 联表查询的基础也是集合运算。SQL 扩展。

我们可以对集合进行如下运算：

并集：对于给定的两个集合，返回一个包含两个集合中所有元素的新集合。
交集：对于给定的两个集合，返回一个包含两个集合中共有元素的新集合。
差集：对于给定的两个集合，返回一个包含所有存在于第一个集合且不存在于第二个集合的元素的新集合。
子集：验证一个给定集合是否是另一集合的子集。

并集

两个集合可以相”加“。A 和 B 的并集是将 A 和 B 的元素放到一起构成的新集合。

集合 A 和集合 B 的并集表示如为 A ∪ B。

并集定义

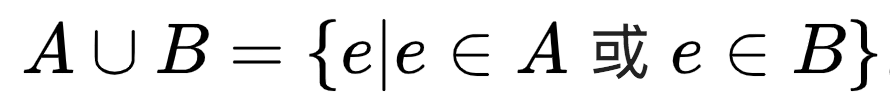
意思是元素 x 存在于 A 中，或 x 存在于 B 中。下图展示了并集运算:

在 Set 类中实现并集的方法 union

class Set {
  // 省略已经定义的方法
  /**
   * 并集
   */
  union(otherSet) {
    // 首先需要创建一个新的集合，代表两个集合的并集（不更改原有集合）
    const unionSet = new Set();
    // 获取第一个集合（当前的 Set 类实例）所有的值（values）
    // 迭代并全部添加到代表并集的集合 unionSet 中
    this.values().forEach((value) => unionSet.add(value));
    // 然后对第二个集合同样遍历添加到并集的集合 unionSet 中
    otherSet.values().forEach((value) => unionSet.add(value));
    // 最后返回结果
    return unionSet;
  }
}

测试：

const setA = new Set();
setA.add(1);
setA.add(2);
setA.add(3);

const setB = new Set();
setB.add(3);
setB.add(4);
setB.add(5);
setB.add(6);
const unionAB = setA.union(setB);
console.log(unionAB.values());

输出为 [1, 2, 3, 4, 5, 6]。注意元素同时存在于 setA 和 setB 中，它在结果集合中只出现一次。

交集

一个新的集合也可以通过两个集合"共"有的元素来构造。A 和 B 的交集，是既属于 A的、又属于 B 的所有元素组成的集合。

交集定义

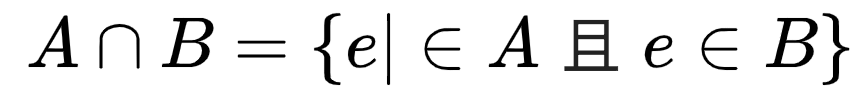
意思是元素 x 存在于 A 中，且 x 存在于 B 中。下图展示了交集运算：

实现 Set 类的 intersection 方法

class Set {
  /**
   * 交集
   */
  intersection(otherSet) {
    // 需要找到当前 Set 实例中所有也存在于给定 Set 实例（otherSet）中的元素
    // 新的集合来存放 intersection 方法的返回结果
    const intersectionSet = new Set();
    // 获取当前集合实例中的值
    const values = this.values();
    // 获取其他集合实例中的值
    const otherValues = otherSet.values();
    // 假设当前的集合 biggerSet 元素较多
    let biggerSet = values;
    // 另一个集合 smallerSet 元素较少
    let smallerSet = otherValues;
    // 比较两个集合的元素个数
    if (otherValues.length - values.length > 0) {
      // 如果另一个集合元素个数多于当前集合的话，交换 biggerSet 和 smallerSet 的值
      biggerSet = otherValues;
      smallerSet = values;
    }
    // 迭代较小集合来计算出两个集合的共有元素并返回
    smallerSet.forEach((value) => {
      if (biggerSet.includes(value)) {
        intersectionSet.add(value);
      }
    });
    return intersectionSet;
  }
}

测试：

const setA = new Set();
setA.add(1);
setA.add(2);
setA.add(3);

const setB = new Set();
setB.add(2);
setB.add(3);
setB.add(4);
const intersectionAB = setA.intersection(setB);
console.log(intersectionAB.values());

输出为 [2, 3]，因为 2 和 3 同时存在于两个集合中。

差集

两个集合也可以相"减"。A 在 B 中的相对补集，集合 A 和集合 B 的差集表示为 A - B。定义如下:

差集定义

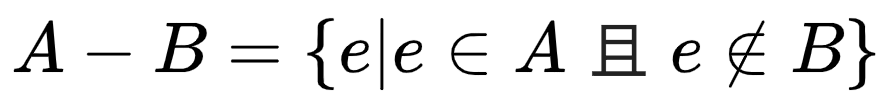
意思是元素 x 存在于 A 中，且 x 不存在于 B 中。下图展示了集合 A 和集合 B 的差集运算:

现在来实现 Set 类的 difference 方法

class Set {
  /**
   * 差集
   */
  difference(otherSet) {
    // difference 方法会得到所有存在于集合 A 但不存在于集合 B 的元素
    // 创建结果集合
    const differenceSet = new Set();
    // 要迭代集合中的所有值
    this.values().forEach((value) => {
      // 检查当前值(元素)是否存 在于给定集合中，
      if (!otherSet.has(value)) {
        // 如果不存在于 otherSet 中，则将此值加入结果集合中Î
        differenceSet.add(value);
      }
    });
    return differenceSet;
  }
}

测试：

const setA = new Set();
setA.add(1);
setA.add(2);
setA.add(3);

const setB = new Set();
setB.add(2);
setB.add(3);
setB.add(4);
const differenceAB = setA.difference(setB);
console.log(differenceAB.values());

输出为 [1]，因为 1 是唯一一个仅存在于 setA 的元素。如果我们执行 setB.difference(setA)，会得到 [4] 作为输出结果，因为 4 是只存在于 setB 中的元素。

子集

例如集合 A 是集合 B 的子集(或集合 B 包含集合 A)，表示： A ⊆ B。集合定义如下：

子集定义

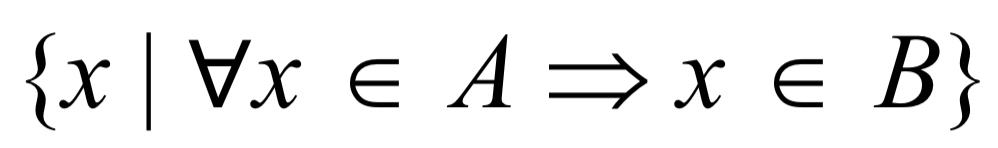
意思是集合 A 中的每一个 x (元素)，也需要存在于集合 B 中。下图展示了集合 A 是集合 B 的子集。

现在来实现 Set 类的 isSubsetOf 方法

class Set {
  /**
   * 子集
   */
  isSubsetOf(otherSet) {
    // 首先需要验证的是当前 Set 实例的大小。
    // 如果当前实例中的元素比 otherSet 实例更多，它就不是一个子集
    // 子集的元素个数需要小于或等于要比较的集合
    if (this.size() > otherSet.size()) {
      return false;
    }
    // 如果当前实例是给定集合的子集
    let isSubset = true;
    // 迭代当前集合的所有元素
    this.values().every((value) => {
      // 验证这些元素是否也存在于 otherSet 中
      if (!otherSet.has(value)) {
        // 如果有任何元素不存在于 otherSet 中，就意味着它不是一个子集，返回 false
        isSubset = false;
        return false;
      }
      // 如果所有元素都存在于 otherSet 中，那么就返回 true
      return true;
    });
    return isSubset;
  }
}

测试：

const setA = new Set();
setA.add(1);
setA.add(2);

const setB = new Set();
setB.add(1);
setB.add(2);
setB.add(3);

const setC = new Set();
setC.add(2);
setC.add(3);
setC.add(4);
console.log(setA.isSubsetOf(setB));
console.log(setA.isSubsetOf(setC));

setA 是 setB 的子集(因此输出为 true)，然而 setA 不是 setC 的子集 (setC 只包含了 setA 中的 2，而不包含 1)，因此输出为 false。

Set 类的完整代码

export default class Set {
  constructor() {
    this.items = {};
  }

  add(element) {
    if (!this.has(element)) {
      this.items[element] = element;
      return true;
    }
    return false;
  }

  delete(element) {
    if (this.has(element)) {
      delete this.items[element];
      return true;
    }
    return false;
  }

  has(element) {
    return Object.prototype.hasOwnProperty.call(this.items, element);
  }

  values() {
    return Object.values(this.items);
  }

  union(otherSet) {
    const unionSet = new Set();
    this.values().forEach((value) => unionSet.add(value));
    otherSet.values().forEach((value) => unionSet.add(value));
    return unionSet;
  }

  intersection(otherSet) {
    const intersectionSet = new Set();
    const values = this.values();
    const otherValues = otherSet.values();
    let biggerSet = values;
    let smallerSet = otherValues;
    if (otherValues.length - values.length > 0) {
      biggerSet = otherValues;
      smallerSet = values;
    }
    smallerSet.forEach((value) => {
      if (biggerSet.includes(value)) {
        intersectionSet.add(value);
      }
    });
    return intersectionSet;
  }

  difference(otherSet) {
    const differenceSet = new Set();
    this.values().forEach((value) => {
      if (!otherSet.has(value)) {
        differenceSet.add(value);
      }
    });
    return differenceSet;
  }

  isSubsetOf(otherSet) {
    if (this.size() > otherSet.size()) {
      return false;
    }
    let isSubset = true;
    this.values().every((value) => {
      if (!otherSet.has(value)) {
        isSubset = false;
        return false;
      }
      return true;
    });
    return isSubset;
  }

  isEmpty() {
    return this.size() === 0;
  }

  size() {
    return Object.keys(this.items).length;
  }

  clear() {
    this.items = {};
  }

  toString() {
    if (this.isEmpty()) {
      return '';
    }
    const values = this.values();
    let objString = `${values[0]}`;
    for (let i = 1; i < values.length; i++) {
      objString = `${objString}, ${values[i].toString()}`;
    }
    return objString;
  }
}

ES6 中的 Set 类

在 ES6 中新增了 Set 类和前面定义的 Set 不同：

ES6 的 Set 的 values 方法返回 Iterator，而不是值构成的数组。
另一个区别是，我们实现的 size 方法返回 set 中存储的值的个数，而 ES6 的 Set 则有一个 size 属性。

const set = new Set();
set.add(1);
console.log(set.values()); // 输出@Iterator
console.log(set.has(1)); // 输出 true
console.log(set.size); // 输出 1
set.delete(1); // 用 delete 方法删除 set 中的元素
set.clear(); // 清除所有成员，没有返回值

ES6 Set 类的运算

Set 类实现了并集、交集、差集、子集等数学运算，然而 ES2015 原生的 Set 并没有这些功能。不过也可以模拟。比如有下面两个集合：

const setA = new Set();
setA.add(1);
setA.add(2);
setA.add(3);

const setB = new Set();
setB.add(2);
setB.add(3);
setB.add(4);

1. 模拟并集运算

创建一个函数，来返回包含 setA 和 setB 中所有的元素的新集合。迭代这两个集合，把所有元素都添加到并集的集合中。代码如下：

const union = (setA, setB) => {
  const unionAb = new Set();
  setA.forEach((value) => unionAb.add(value));
  setB.forEach((value) => unionAb.add(value));
  return unionAb;
};
console.log(union(setA, setB)); // 输出 [1, 2, 3, 4]

2. 模拟交集运算 模拟交集运算需要创建一个辅助函数，来生成包含 setA 和 setB 共有元素的新集合。代码如下：

const intersection = (setA, setB) => {
  const intersectionSet = new Set();
  setA.forEach((value) => {
    if (setB.has(value)) {
      intersectionSet.add(value);
    }
  });
  return intersectionSet;
};

//

console.log(intersection(setA, setB)); // 输出 [2, 3]

3. 模拟差集运算

交集运算创建的集合包含 setA 和 setB 都有的元素，差集运算创建的集合则包含 setA 有而 setB 没有的元素。看下面的代码：

const difference = (setA, setB) => {
  const differenceSet = new Set();
  setA.forEach((value) => {
    // intersection 函数和 difference 函数除函数名外只有一行不同
    if (!setB.has(value)) {
      differenceSet.add(value);
    }
  });

  return differenceSet;
};

console.log(difference(setA, setB));

4. ES6 的扩展运算符方式实现并集、交集和差集

步骤为：(1) 将集合转化为数组; (2) 执行需要的运算; (3) 将结果转化回集合。

// 并集
const union = (setA, setB) => new Set([...setA, ...setB]);
// 交集
const intersection = (setA, setB) => new Set([...setA].filter((x) => setB.has(x)));
// 差集
const difference = (setA, setB) => new Set([...setA].filter((x) => !setB.has(x)));

信息

广义的集合种类包括列表，集，多重集，树和图。枚举类型可以是列表或集。这里主要讲的是集（即数学里的集合），而非广义的集合 (计算机科学)。

实现集合类​

测试 Set 类​

集合运算​

并集​

交集​

差集​

子集​

Set 类的完整代码​

ES6 中的 Set 类​

ES6 Set 类的运算​