算法复杂度
大 O 表示法
它用于描述算法的性能和复杂程度。大 O 表示法将算法按照消耗的时间进行分类,依据随输入增大所需要的空间/内存。
如何衡量算法的效率?通常是用资源,例如 CPU(时间)占用、内存占用、硬盘占用和网 络占用。当讨论大 O 表示法时,一般考虑的是 CPU(时间)占用。所以资源包括时间资源和内存资源。
分析算法时,时常遇到以下几类函数。
| 符号 | 名称 |
|---|---|
| O(1) | 常数的 |
| O(log(n)) | 对数的 |
| O((log(n))c) | 对数多项式的 |
| O(n) | 线性的 |
| O(n2) | 二次的 |
| O(nc) | 多项式的 |
| O(cn) | 指数的 |
时间复杂度比较
| 输入大小(n) | O(1) | O(log(n)) | O(n) | O(nlog(n)) | O(n2) | O(2n) |
|---|---|---|---|---|---|---|
| 10 | 1 | 1 | 10 | 10 | 100 | 1024 |
| 20 | 1 | 1.30 | 20 | 26.02 | 400 | 1 048 576 |
| 50 | 1 | 1.69 | 50 | 84.94 | 2500 | 非常大 |
| 100 | 1 | 2 | 100 | 200 | 10 000 | 非常大 |
| 500 | 1 | 2.69 | 500 | 1349.48 | 250 000 | 非常大 |
| 1000 | 1 | 3 | 1000 | 3000 | 1 000 000 | 非常大 |
| 10 000 | 1 | 4 | 10 000 | 40 000 | 100 000 000 | 非常大 |
可以基于上表信息画一个图来表示不同的大 O 表示法的消耗。
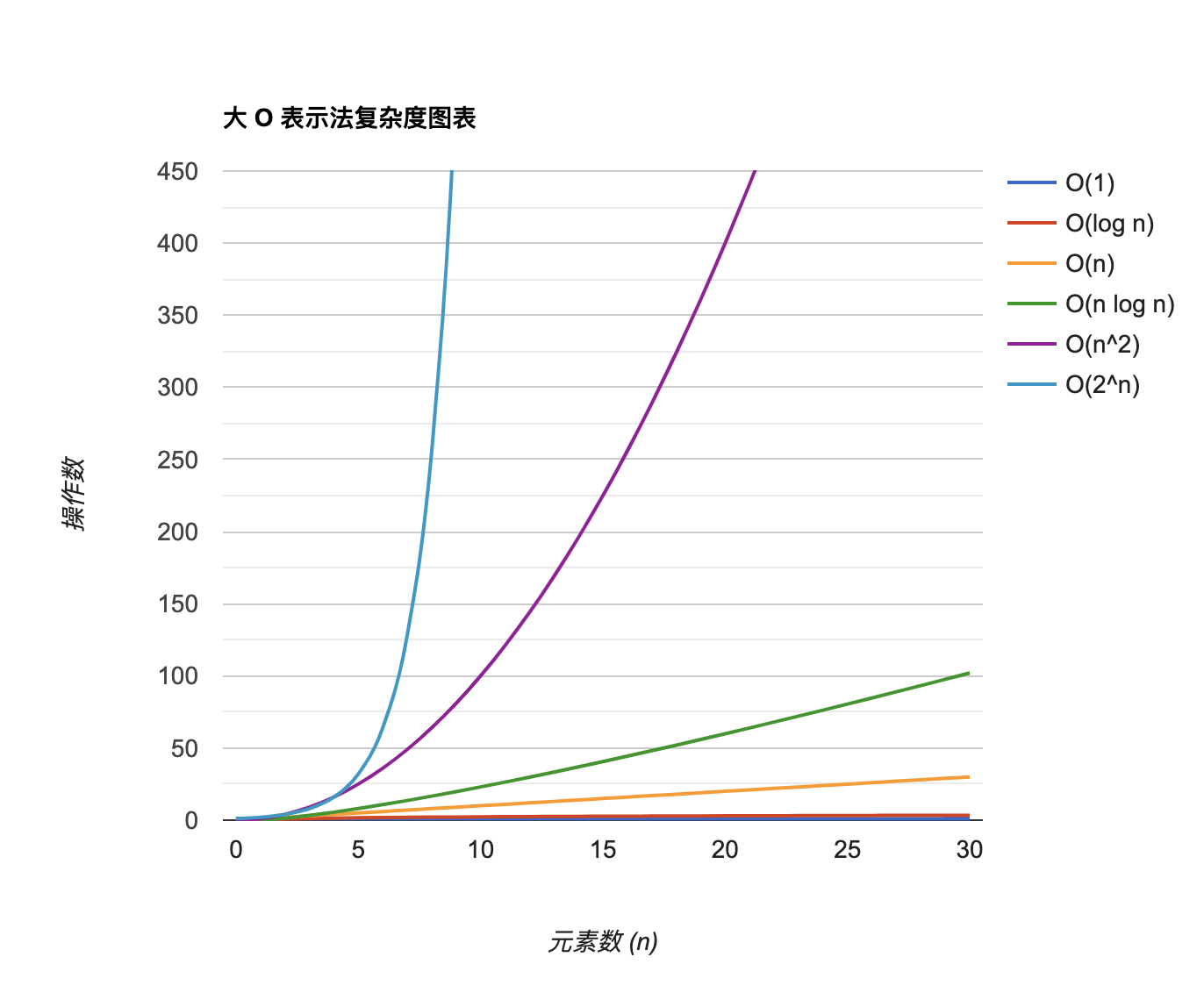
下面为常用算法和数据结构的时间复杂度:
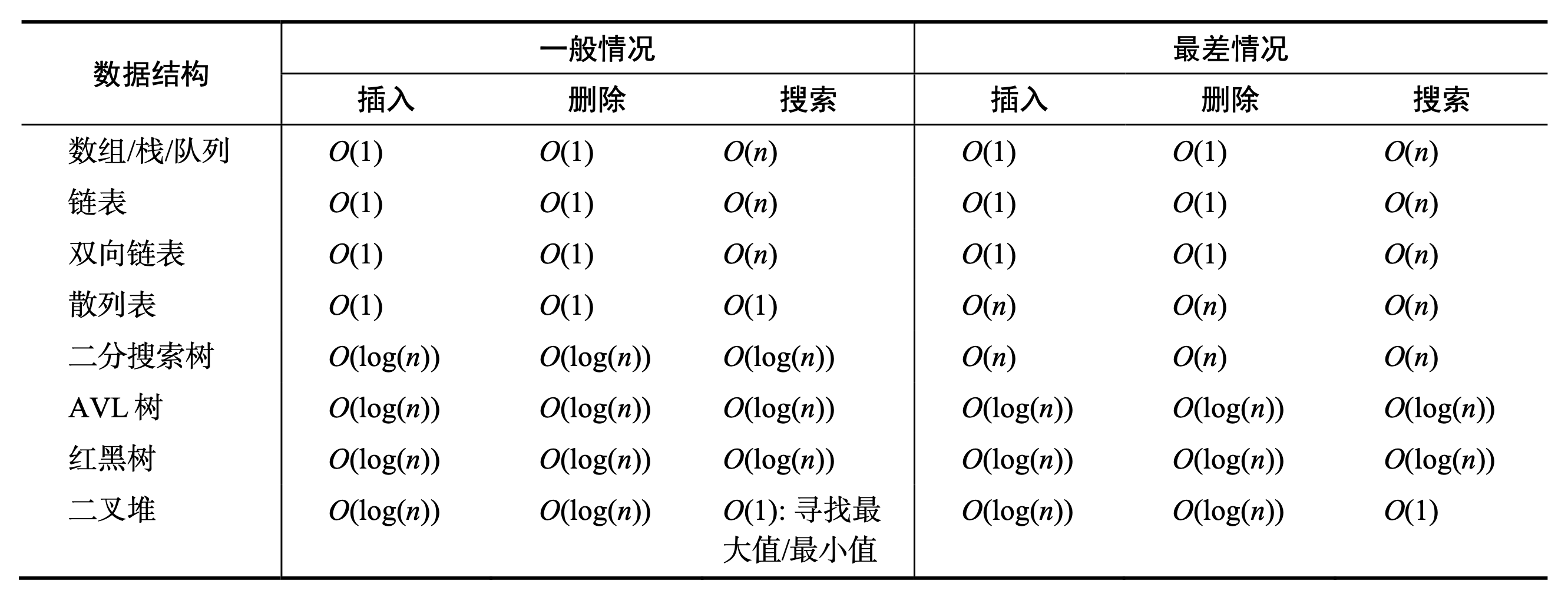
1. 数据结构
下表是常用数据结构的时间复杂度:
2. 图
下表是图的时间复杂度。

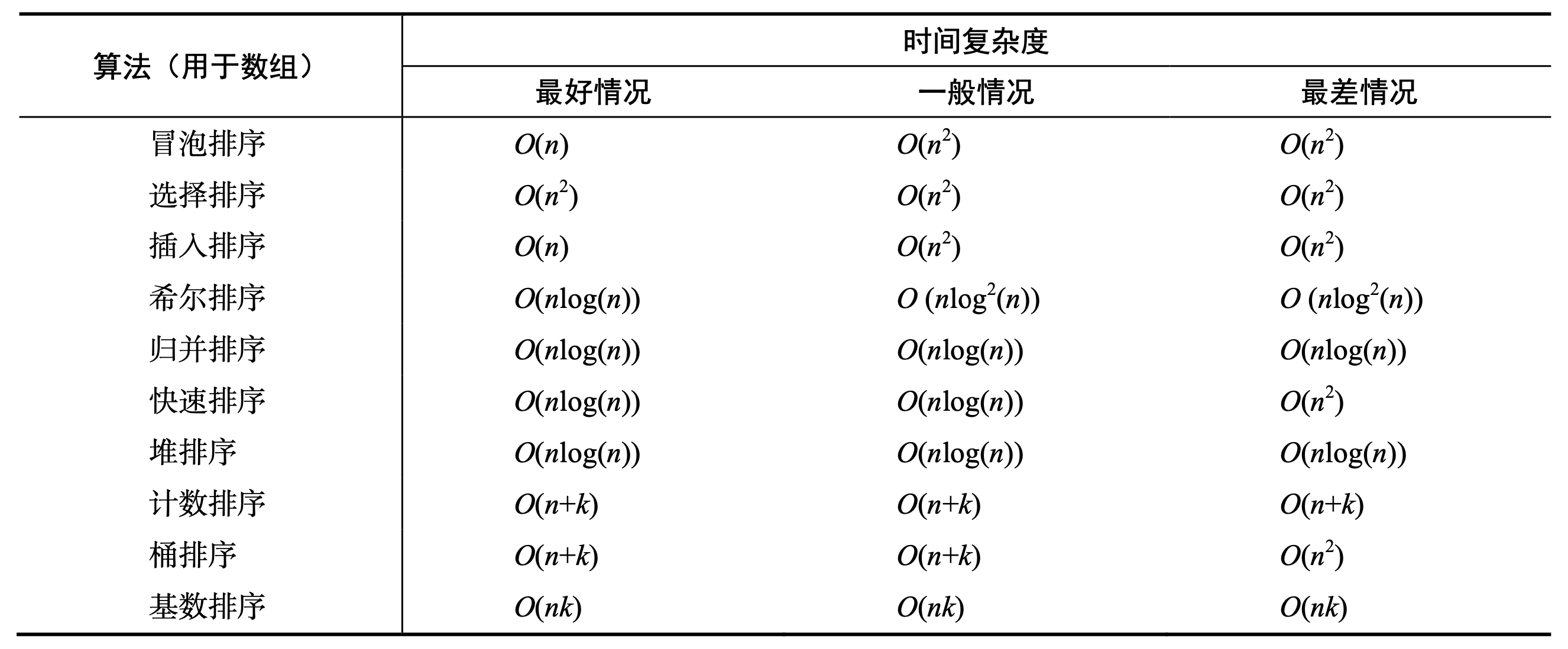
3. 排序算法
下表是排序算法的时间复杂度。
4. 搜索算法
下表是搜索算法的时间复杂度:
